Wavelet-based grid-adaptation for nonlinear scheduling subject to time-variable electricity prices

Abstract

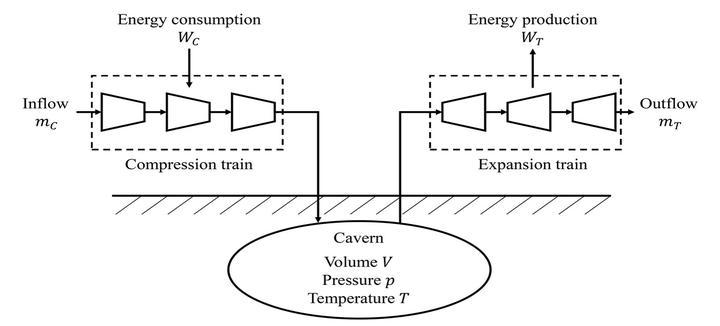
Using nonlinear process models in discrete-time scheduling typically prohibits long planning horizons with fine temporal discretizations. Therefore, we propose an adaptive grid algorithm tailored for scheduling subject to time-variable electricity prices. The scheduling problem is formulated in a reduced space. In the algorithm, the number of degrees of freedom is reduced by linearly mapping one degree of freedom to multiple intervals with similar electricity prices. The mapping is iteratively refined using a wavelet-based analysis of the previous solution. We apply the algorithm to the scheduling of a compressed air energy storage. We model the efficiency characteristics of the turbo machinery using artificial neural networks. Using our in-house global solver MAiNGO, the algorithm identifies a feasible near-optimal solution with  < 1% deviation in the objective value within  < 5% of the computational time compared to a solution considering the full dimensionality.