Abstract
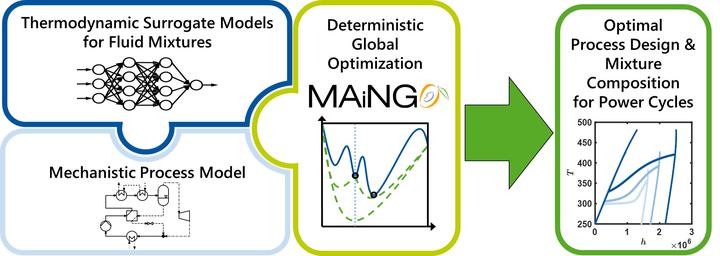
Numerical optimization is very useful for design and operation of energy processes. As the design has a major impact on the economics of the system, it is desirable to find a global optimum in the presence of local optima. So far, deterministic global optimization with detailed thermodynamic models incorporated has been limited to single fluid energy systems. We extend our previously presented approach [Schweidtmann et int Mitsos, COMPUT CHEM ENG (2019)] from single-species working fluids to binary mixtures with variable composition. First, we create accurate thermodynamic data for two selected binary mixtures using a thermodynamic library. Using this data, we train artificial neural networks, select them based on desired accuracy, and include them in the process model. The resulting hybrid model is then optimized with the open-source solver MAiNGO. We perform thermodynamic optimizations of geothermal power plants, considering both organic Rankine and Kalina cycle. For each cycle, we identify the globally optimal design, operation, and working fluid composition for the selected binary fluid mixtures within tractable CPU times. We show how a second mixture component enables improved ORC performance.