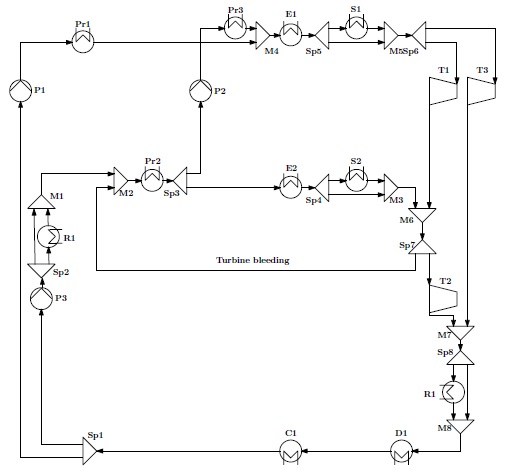
Abstract
Organic Rankine cycles (ORCs) offer a high structural design flexibility. The best process structure can be identified via the optimization of a superstructure, which considers design alternatives simultaneously. In this contribution, we apply deterministic global optimization to a geothermal ORC superstructure, thus guaranteeing to find the best solution. We implement a hybrid mechanistic data-driven model, employing artificial neural networks as thermodynamic surrogate models. This approach is beneficial as we optimize the problem in a reduced space using the optimization solver MAiNGO. We further introduce redundant constraints that are only considered for the lower-bounding problem of the branch-and-bound algorithm. We perform two separate optimizations, one maximizing power output and one minimizing levelized cost of electricity. The optimal solutions of both objectives differ from each other, but both have three pressure levels. Global optimization is necessary as there exist suboptimal local solutions for both flowsheet configuration and design with fixed configurations.