Efficient multiobjective optimization employing Gaussian processes, spectral sampling and a genetic algorithm
Abstract
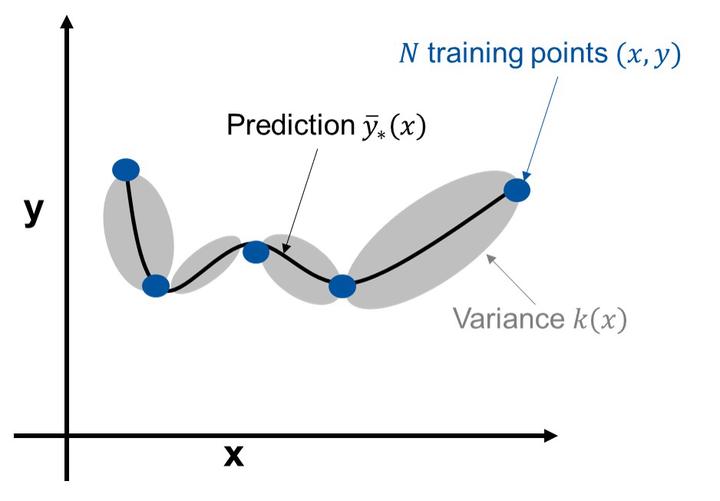
Many engineering problems require the optimization of expensive, black-box functions involving multiple conflicting criteria, such that commonly used methods like multiobjective genetic algorithms are inadequate. To tackle this problem several algorithms have been developed using surrogates. However, these often have disadvantages such as the requirement of a priori knowledge of the output functions or exponentially scaling computational cost with respect to the number of objectives. In this paper a new algorithm is proposed, TSEMO, which uses Gaussian processes as surrogates. The Gaussian processes are sampled using spectral sampling techniques to make use of Thompson sampling in conjunction with the hypervolume quality indicator and NSGA-II to choose a new evaluation point at each iteration. The reference point required for the hypervolume calculation is estimated within TSEMO. Further, a simple extension was proposed to carry out batch-sequential design. TSEMO was compared to ParEGO, an expected hypervolume implementation, and NSGA-II on nine test problems with a budget of 150 function evaluations. Overall, TSEMO shows promising performance, while giving a simple algorithm without the requirement of a priori knowledge, reduced hypervolume calculations to approach linear scaling with respect to the number of objectives, the capacity to handle noise and lastly the ability for batch-sequential usage.